欧氏空间的切向量空间
点击：
摘要：欧氏空间的切向量空间 上图是以xi为函数，求出点q在基δi下的坐标xi。 上图是对于二维欧氏空间而言。 这里vi是求导后得到的结果。 这里的vi是在坐标轴xi下的坐标，而 表示一个坐标函
欧氏空间的切向量空间
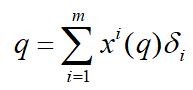
上图是以xi为函数，求出点q在基δi下的坐标xi。
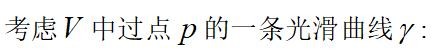
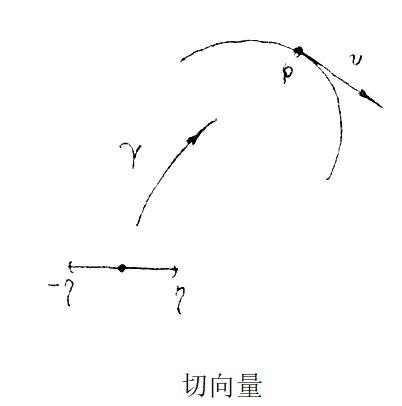
上图是对于二维欧氏空间而言。
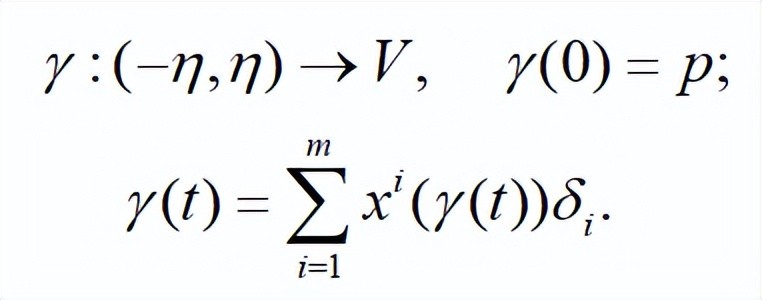
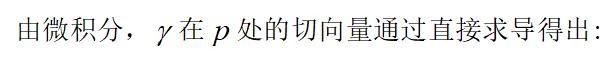
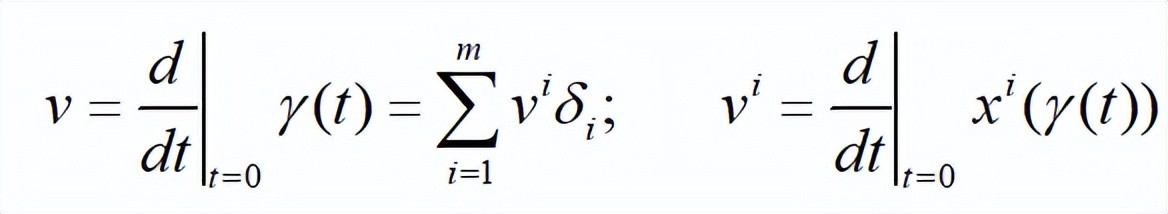
这里vi是求导后得到的结果。
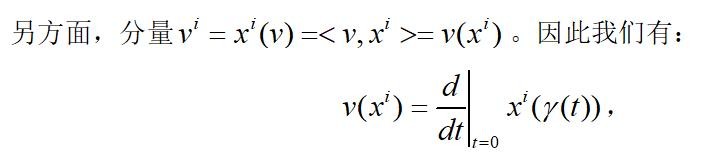
这里的vi是在坐标轴xi下的坐标，而
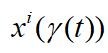
表示一个坐标函数，这个函数以γ(t)为参数。
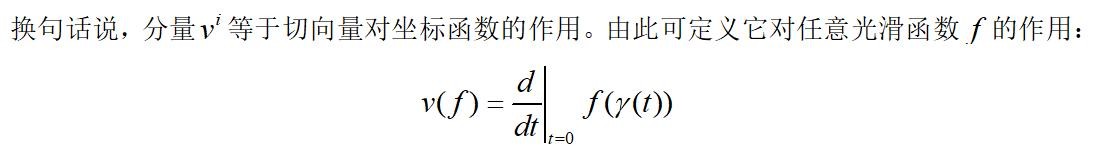
这里是将上面的坐标函数扩展为任意函数，它是线性的。
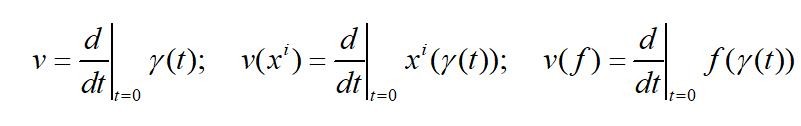
然而在一般微分流形上定义切向量，只能选择不够直观的第三种；原因很简单，对抽象的
微分流形上的点，不能直接求导。
无论坐标函数还是任意函数，都存在分量。
比较新、旧定义下的表达式：
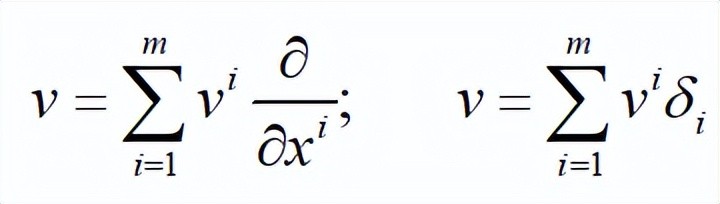
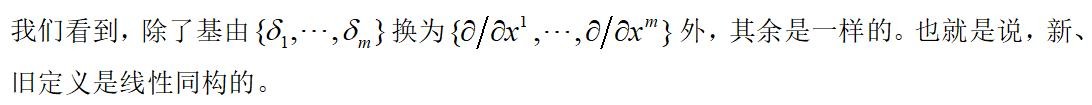
最后，坐标函数和任意函数之间的差异，仅仅是基的不同而已，所以两者是同构的。
相关标签：
