secx等于什么求导(secx等于什么公式)

2025-11-11 21:23 点击：来源：好爱生活

摘要：secx等于什么求导(secx等于什么公式) 在微积分中，求导是一项重要的技巧，用于计算函数在某一点处的斜率。当我们遇到类似于secx这样的函数，我们自然会想知道它的导数是什么。sec

secx等于什么求导(secx等于什么公式)

在微积分中，求导是一项重要的技巧，用于计算函数在某一点处的斜率。当我们遇到类似于secx这样的函数，我们自然会想知道它的导数是什么。secx代表的是余割函数，它是三角函数中的一个重要成员。余割函数的定义是secx=1/cosx，也就是说，它是余弦函数的倒数。那么，当我们对secx进行求导时，我们会得到什么结果呢？这个问题的答案有着一定的复杂性，涉及到一些高级的微积分知识。让我们一起来揭开这个谜团，并探索secx的导数值。

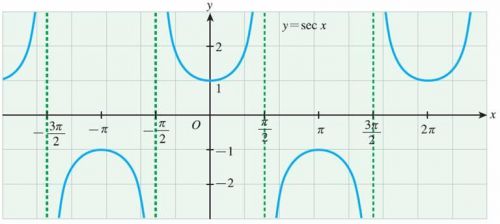
secx等于什么求导(secx等于什么公式)-第1张图片-

1、y=secx的导数是什么？

优质回答1：

y=secx的导数：(secx)’=(1/cosx)’=[1’cosx-(cosx)’]/cos^2x=sinx/cos^2 x=secx*tanx。所以y=secx的导数是secx*tanx。扩展资料导数，也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的'增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。

优质回答2：

导数为: sinx除以cos2x的平方

y＝secx+cscx＝(cosx)^(-1)+(sinx)^(-1)∴y'＝(-1/cos²x)·(cosx)'+(-1/sin²x)·(sinx)'＝(-sinx)/(-cos²x)+(cosx)/(-sin²x)＝(tanx)/(cosx)-(cotx)/(sinx)＝secxtanx-cscxcotx.∴y'＝secxtanx-

2、sec的导数推导？

优质回答1：

secx的导数推导公式是：(secx)’=(1/cosx)’=[1’cosx-(cosx)’]/cos^2 x=sinx/cos^2 x=secx*tanx。所以secx的导数是secx*tanx。

导数的定义：

导数也叫导函数值，是微积分中的主要基础概念，导数是函数的局部性质，一个函数在某一点的导数描述了这个函数在这一点附近的变化率，如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点的切线斜率，导数的本质是通过极限的概念对函数进行局部的线性逼近。

导数实例：当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'(x0)或df(x0)/dx。

不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数，若某函数在某一点导数存在，则称其在这一点可导，否则成为不可导，然而，可导的函数一定连续，不连续的函数一定不可导。

导数求导法则：

1.常为零，幂降次;

2.对倒数(e为底时直接倒数，a为底时乘以1/lna);

3.指不变(特别的，自然对数的指数函数完全不变，一般的指数函数须乘以lna);

4.正变余，余变正;

5.切割方(切函数是相应割函数(切函数的倒数)的平方);

6.割乘切，反分式。

导数的几何意义：

函数y=f(x)在x0点的导数f'(x0)的几何意义：表示函数曲线在点P0(x0,f(x0))处的切线的斜率(导数的几何意义是该函数曲线在这一点上的切线斜率)。

优质回答2：

假设 $f(x)$ 是一个可导函数，那么 $f(x)$ 在 $x$ 处的导数可以表示为：

$$\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$$

对于 $f(x)=\sec(x)$，我们可以使用三角函数的定义来推导它的导数。

首先，我们将 $\sec(x)$ 表示为 $\frac{1}{\cos(x)}$，然后使用商规则求导，即：

$$\begin{aligned} \frac{d}{dx}\sec(x) &= \frac{d}{dx}\frac{1}{\cos(x)} \\ &= -\frac{1}{\cos^2(x)}\frac{d}{dx}\cos(x) \\ &= -\frac{1}{\cos^2(x)}(-\sin(x)) \\ &= \frac{\sin(x)}{\cos^2(x)} \\ &= \frac{\sin(x)}{\cos(x)}\cdot\frac{1}{\cos(x)} \\ &= \tan(x)\sec(x) \end{aligned}$$

因此，$\sec(x)$ 的导数为 $\tan(x)\sec(x)$。

优质回答3：

我们知道，sec(x)表示x的余切值的倒数，即：

sec(x) = 1/cos(x)

因此，可以使用商规则来推导其导数。具体地：

(sec(x))' = [1/cos(x)]'

要计算cos(x)的导数，可以使用链式法则。根据链式法则：

[1/cos(x)]' = (-1/cos^2(x))·(cos(x))'

其中，cos(x)的导数是-sin(x)，因此：

[1/cos(x)]' = (-1/cos^2(x))·(-sin(x))

将其化简得到：

[1/cos(x)]' = sin(x)/cos^2(x)